The loop step is the vector’s length. The following diagram pre-visualizes the code:
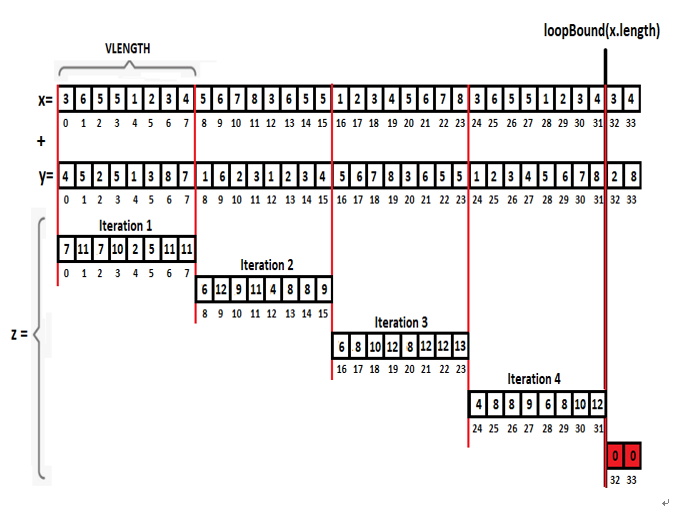
Figure 5.8 – Computing z = x + y in chunks
So, at the first iteration, our vectors will accommodate the scalars from index 0 to 7. At the second iteration, the scalars are from index 8 to 15, and so on. Here is the complete code:
public static void sum(int x[], int y[], int z[]) {
int upperBound = VS256.loopBound(x.length);
for (int i = 0; i < upperBound; i += VS256.length()) {
IntVector xVector = IntVector.fromArray(VS256, x, i);
IntVector yVector = IntVector.fromArray(VS256, y, i);
IntVector zVector = xVector.add(yVector);
zVector.intoArray(z, i);
}
The intoArray(int[] a, int offset) transfers the scalars from a vector to a Java array. This method comes in different flavors next to intoMemorySegment().The resulting array will be: [7, 11, 7, 10, 2, 5, 11, 11, 6, 12, 9, 11, 4, 8, 8, 9, 6, 8, 10, 12, 8, 12, 12, 13, 4, 8, 8, 9, 6, 8, 10, 12, 0, 0]. Check out the last two items … they are equal to 0. These are the items that result from x.length – upperBound = 34 – 32 = 2. When the largest multiple of VLENGTH (vector’s length) is equal to x.length this difference will be 0, otherwise, we will have the rest of the items that were not been computed. So, the previous code will work as expected only in the particular case when VLENGTH (vector’s length) is equal to x.length.Covering the remaining items can be accomplished in at least two ways. First, we can rely on a VectorMask as in the following code:
public static void sumMask(int x[], int y[], int z[]) {
int upperBound = VS256.loopBound(x.length);
int i = 0;
for (; i < upperBound; i += VS256.length()) {
IntVector xVector = IntVector.fromArray(VS256, x, i);
IntVector yVector = IntVector.fromArray(VS256, y, i);
IntVector zVector = xVector.add(yVector);
zVector.intoArray(z, i);
}
if (i <= (x.length – 1)) {
VectorMask<Integer> mask
= VS256.indexInRange(i, x.length);
IntVector zVector = IntVector.fromArray(VS256, x, i, mask)
.add(IntVector.fromArray(VS256, y, i, mask));
zVector.intoArray(z, i, mask);
}
}
The indexInRange() computes a mask in the range [i, x.length-1]. Applying this mask will result in the following z array: [7, 11, 7, 10, 2, 5, 11, 11, 6, 12, 9, 11, 4, 8, 8, 9, 6, 8, 10, 12, 8, 12, 12, 13, 4, 8, 8, 9, 6, 8, 10, 12, 5, 12]. Now, the last two items are computed as expected.
As a rule of thumb, avoid using VectorMask in loops. They are quite expensive and may lead to a significant degradation in performance.
Another approach for dealing with these remaining items is to go for a piece of traditional Java code as follows:
public static void sumPlus(int x[], int y[], int z[]) {
int upperBound = VS256.loopBound(x.length);
int i = 0;
for (; i < upperBound; i += VS256.length()) {
IntVector xVector = IntVector.fromArray(VS256, x, i);
IntVector yVector = IntVector.fromArray(VS256, y, i);
IntVector zVector = xVector.add(yVector);
zVector.intoArray(z, i);
}
for (; i < x.length; i++) {
z[i] = x[i] + y[i];
}
}
Practically, we sum up the remaining items in a Java traditional loop outside the vectors loop. You can check these examples in the bundled code.
